Accelerating Domain Propagation via GPUs
TL;DR: This is an informal discussion of our recent paper Accelerating Domain Propagation: an Efficient GPU-Parallel Algorithm over Sparse Matrices by Boro Sofranac, Ambros Gleixner, and Sebastian Pokutta. In the paper, we present a new algorithm to perform domain propagation of linear constraints on GPUs efficiently. The results show that efficient implementations of Mixed-integer Programming (MIP) methods are possible on GPUs, even though the success of using GPUs in MIPs has traditionally been limited. Our algorithm is capable of performing domain propagation on the GPU exclusively, without the need for synchronization with the CPU, paving the way for the usage of this algorithm in a new generation of MIP methods that run on GPUs.
Written by Boro Sofranac.
The motivation
Since the advent of general-purpose, massively parallel GPU hardware, many fields of applied mathematics have actively sought out the design of specialized algorithms which exploit the unprecedented computational resources this new type of hardware has to offer. A prime example are Neural Networks, whose rise to prominence was fueled by the “Deep Learning revolution” with Deep Learning methods running on GPUs. Still, such success is missing in many other fields which are not as amenable to specialized and massively parallel programming model of the GPUs. One such field is Mixed-integer Programming (MIP).
The development of the Simplex algorithm for solving Linear Programs (LPs) in the 1940s was followed by a plethora of methods and solvers to solve LPs and MIPs over the following decades. A unifying characteristic of these methods is a) that they exhibit non-uniform algorithmic behaviour, and b) they operate on highly irregular data (i.e., data structures are sparse and do not have a regular structure in general). Such characteristics make the implementation of these methods on massively parallel hardware challenging and have hindered the application of GPUs in the field.
Recognizing these challenges in a number of fields, GPU hardware development in recent years has been geared towards easier expression of non-uniform workflows in its programming model (for example, the Dynamic Parallelism feature of NVIDIA GPUs) and hardware (e.g., atomic operations). At the same time, researchers working in some related fields have shown that with the right algorithmic design GPUs can be efficiently used for workflows previously considered unsuitable due to challenges similar to those present in MIP methods. Consider for example Numerical Linear Algebra (LA): for years, dense LA has been one of the main benefactors of GPU computing and allowed for tremendous speedups. On the other hand, if the input data was sparse (and irregular), the same algorithms often exhibited disappointing performance. New algorithms however, such as the CSR-Adaptive algorithm developed by Greathouse and Daga to perform sparse matrix-vector products (SpMV) have shown very impressive performance gains for highly unstructured sparse matrices.
Against this backdrop, we set out to investigate the applicability of massively parallel algorithms in MIP methods. This, however, is no simple task: massively parallel programming models bring with them a different algorithmic paradigm and complexity notions while MIP methods have historically been strongly sequential. Basic design decisions need to be rethought and/or new algorithms developed. So we took a core MIP method used by all state-of-the-art solvers, namely Domain Propagation, which is traditionally not amenable to efficient parallelization, and we show that with the right algorithmic design speedups seen in fields such as sparse Linear Algebra are also possible here. This new GPU algorithm for Domain Propagation and computational experiments assessing the performance are presented in our paper; the code is available on our GitHub page.
Sneak peek at the results
We use the de-facto standard MIPLIB2017 test set for MIPs to conduct our experiments. To better capture the response of our algorithm to the size of instances, we subdivided this set into 8 subsets with instances of increasing size, dubbed Set-1 to Set-8. For comparison, we use four algorithms:
- cpu_seq is a sequential implementation of domain propagation which closely follows implementations in state-of-the-art solvers.
- cpu_omp is a shared-memory parallel version of domain propagation which runs on the CPU.
- gpu_atomic is our GPU implementation with atomic operations
- gpu_reduction is our GPU implementation which avoids using atomic operations by using reductions in global memory.
The algorithms are tested on the following hardware:
- V100 NVIDIA Tesla V100 PCIe 32GB (GPU)
- RTX NVIDIA Titan RTX 24GB (GPU)
- P400 NVIDIA Quadro P400 2GB (GPU)
- amdtr 64-core AMD Ryzen Threadripper 3990X @ 3.30 GHz with 128 GB RAM (CPU)
- xeon 24-core Intel Xeon Gold 6246 @ 3.30GHz with 384 GB RAM (CPU)
As baseline, we choose the execution cpu_seq algorithm on the xeon machine. As the metric for comparison, we will report speedups of all other executions over this base case.
Figure 1-a shows the geometric mean of speedups of the four algorithms over the test subsets. Figure 1-b shows the distribution of speedups of the four algorithms over all the instances in the test set, sorted in ascending order by speedup.
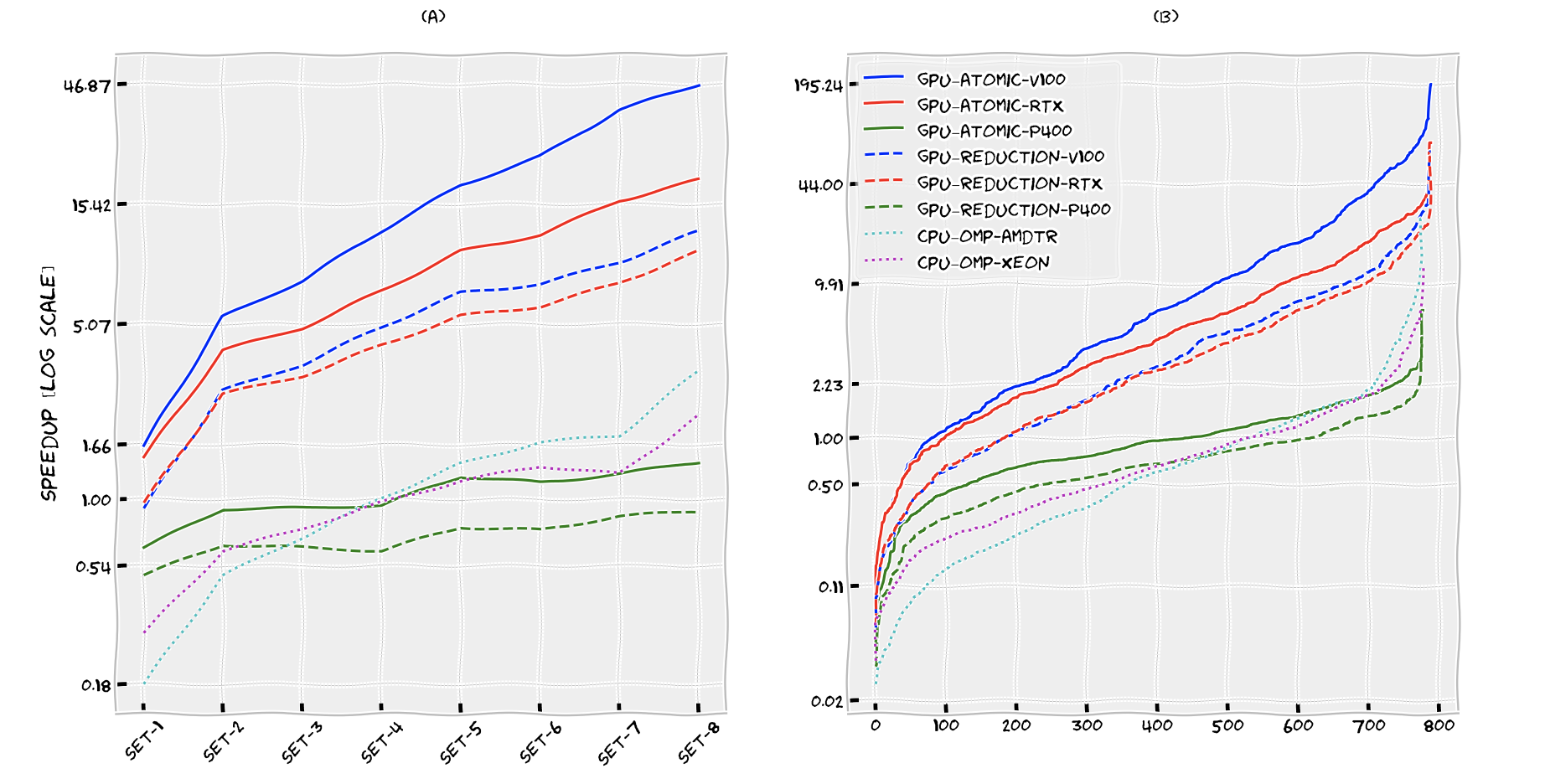
Figure 1. a) Geometric means of speedups b) speedup distributions in ascending order.
We can see that GPU algorithms on high-end hardware V100 and RTX drastically outperform the sequential and shared memory executions. Additionally, the GPU algorithms with atomic operations outperform the reduction version in all executions. The fastest combination is the gpu_atomic algorithm on V100. Its mean speedup is always greater than 1.6 and goes up to 46.9 in Set-8, following a roughly linear trend. Over the entire test set, the mean speedup is 6.1. For the top 5% of the instances, this execution achieves a speedup of at least 62.9 times. As we can see in Figure 1-b, speedups as high as 195x are possible.
A low-end, consumer-grade GPU P400, often found in home-use desktops, is also evaluated in the tests. It is evident from the plots that it cannot keep up with the two high-end GPUs. However, we can see that gpu_atomic running on P400 is still competitive with the CPU implementation for about half the instances, where it achieves a small speedup over the benchmark cpu implementation. This result is interesting considering that GPUs are currently a resource that is not used by MIP solvers at all, opening up the possibility for using GPUs as co-processors for MIP solvers even on standard desktop machines.
Looking at the shared-memory parallel cpu_omp algorithm, we can see that it also is drastically outperformed by the GPU implementations on V100 and RTX. Comparing it to the sequential base case, it underperforms in about half of the instances. The parallelism found in the domain propagation algorithm is relatively fine-grained, with low-arithmetic intensity in the parallel units of work. This does not bode well for the shared-memory parallelization on the CPU where managing CPU threads is comparatively expensive, explaining why current state-of-the-art implementations of Domain Propagation are usually single thread only
Conclusions
In conclusion, the domain propagation algorithm on the GPU achieves ample speedups over its CPU counterparts, over the majority of practically relevant instances. Beyond being interesting in its own right, it does not tell the whole story! The throughput-based GPU programming model differs significantly from the latency-based sequential model, and comparing the runtimes of parts of the solving process alone might not give justice to the GPU paradigm. Our algorithm runs entirely on the GPU, without the need for synchronization with the CPU, which paves the way to embedding this algorithm in future GPU-based MIP solvers/methods. Put differently, the massive amounts of parallelism on the GPU bring about a different paradigm, with the potential to achieve more than speeding up parts of an otherwise sequential workflow.
Comments